那些奇怪的排序算法，你见过吗？

---

如果有人问你哪种排序算法最奇怪，可能你会先在冒泡排序、选择排序、快速排序等常见排序算法中「搜索」了。

 

有人在 Quora 上也发帖问了这个问题。于是乎，各种脑洞大开的奇特算法就被列出来了。它们可能存在性能问题或无法实现，但是不可否认其创造性。

 

 

 

睡眠排序（Nipun Ramakrishnan 的回答）

 

 

这个搞笑算法流传于 4chan 的 /prog/ 板块。无从查证具体出自哪位程序员，伪代码如下

 

procedure printNumber(n)

    sleep n seconds

    print n

end

 

for arg in args

    run printNumber(arg) in background

end

wait for all processes to finish

 

算法运行如下： 对于数组中每个元素 x，开启一个新程序：

 

休眠 x 秒

 

打印 x 所有元素同时开始计时。 只适用于非负数字。

 

 

Bogo 排序/猴子排序 （Ryan Turner的回答）

 

Bogo 排序/猴子排序，名字很奇怪。它是愚蠢排序中的一员。

 

主要来说，算法就是你把元素随机排列。

 

如果没有排好序，再次把元素随机排列。

 

如果还没有排好序，你懂的。下面是个例子：

 

4, 7, 9, 6, 5, 5, 2, 1 (未排序)

2, 5, 4, 7, 5, 9, 6, 1 (随机排列)

1, 4, 5, 6, 9, 7, 5, 2 (再次随机排列)

1, 2, 4, 5, 5, 6, 7, 9 (天呐，真幸运)

 

你不停地随机排序，直到得到一个有序数组。

 

毫无疑问这是最低效的排序算法之一，除非你非常非常幸运。它时间复杂度是令人窒息的 O(n!)，而且随着元素数量增加，很有 O(∞) 的趋势。

 

 

量子 Bogo 排序（Tyler Schroeder 的回答）

 

我是量子 Bogo 排序的粉丝：

 

随机排列数组中元素。

 

如果数组没有排好序，摧毁当前宇宙（这一步就拜托你了）

 

存活的宇宙将会有排好序的数组。 时间复杂度仅仅 O(n) 注意：这种算法依赖于量子力学的平行宇宙理论的可靠性。如果量子力学的平行宇宙理论不准确，这个算法时间复杂度达不到 O(n)

 

 

打印店页码排序 （Yi Wang的回答）

 

这并不是我发明的，我从别处看到的。

 

一个学生去打印店打印材料。他需要两份，但并没有直接打印两份，而是将每一页打印了两次，像下面这样：

 

需要的页码顺序: 1 2 3 4 … N; 1 2 3 4 … N

 

手上的页码顺序: 1 1 2 2 3 3 4 4 …. N N

 

他开始对打印材料排序，取一页放在左边，然后取一页放在右边。打印店老板看不下去了，直接把材料拿过来。

 

老板首先取一页放在左边，然后两页放在右边，再然后两页左边，两页右边…… 排序速度瞬间翻倍 ……

 

（有网友评论提醒：这是归纳，不是排序）

 

 

下面是其他网友的回答：

 

慢排序

 

这是一个非常幽默却没什么用的排序算法。它基于“合而不治”的原则（分治算法基本思想“分而治之”的反义词，文字游戏），它由 Andrei Broder 和 Jorge Stolfi 于 1986 年发表在论文《Pessimal Algorithms and Simplexity Analysis（最坏排序和简单性分析）》中，伪代码如下：

 

function slowSort(array,start,end){

    if( start >= end ) return; //已经不能再慢了

    middle = floor( (start+end)/2 );

    //递归

    slowSort(array,start,middle);

    slowSort(array,middle+1,end);

    //比较得出最大值放在队尾

    if( array[end] < array[middle] )

        swap array[end] and array[middle]

    //去掉最大值之后再排序

    slowsort(array,start,end–1);

}

 

递归排序好前一半

 

递归排序好后一半

 

比较中间和队尾的值，得到整个数组的最大值，将最大值放到队尾。

 

去掉最大值，递归整个数组

 

 

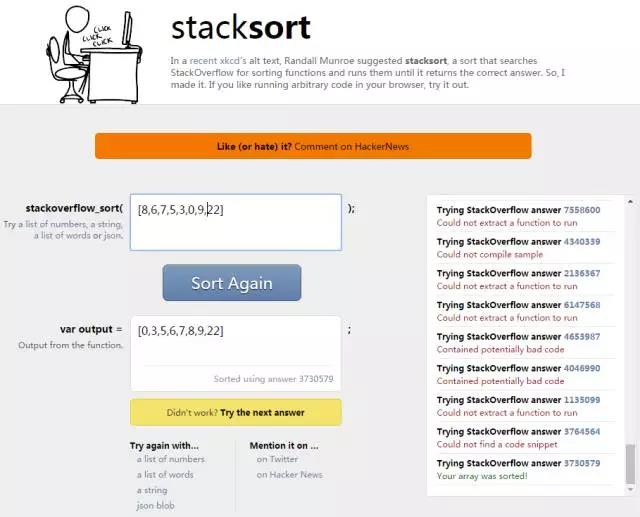
Stack 排序

 

从 StackOverflow 上搜索标题含有“数组排序”的帖子，复制粘贴并运行其中的代码片段，直到数组排好序。我认为这种排序算法事实上验证了整个数组。它被发表在xkcd网站上，这里有一个在线版的具体实现stacksort

 

 

 

随机排序

 

运行如下： 创建一个随机程序。 传入数组并运行随机程序。 如果程序的输出恰好是排好序的，完成。 否则重复上面过程。

 

 

太阳能比特翻转排序

 

太阳发出的阿尔法粒子偶尔能够翻转内存中的比特位，所以这种算法主要基于希望这种翻转能够使元素正确排序。运行方式如下：

 

检查数组是否排好序。 如果排好序，返回这个数组。 如果没有，等 10 秒钟并祈祷太阳辐射使得比特位翻转，而且使得数组排好序，重复第一步。

 

 

意大利面排序

 

这是一种线性时间算法，是需要 O(n) 空间的稳定排序。它需要并行处理器。简单来说，假设我们排序一列自然数。排序方法需要使用很多根生的意大利面条。

 

 

 

将数据按比例转换成表示意大利面条长度的数字。 在每根面条上写下数字，并将面条折断成数字表示的长度。 把所有面条攥成一捆并把底部在平面上敲击。 取出最突出的一根面条，也就是最长的一根，获取上面的数字，转换成原始的数据并记录下来。 重复这个过程直到处理完所有意大利面。

 

 

指鹿为马排序

 

这个算法时间复杂度 O(n)。 聚集一帮人并向他们展示数组。 询问他们这个数组是否是排序好的。 干掉其中认为没有排序好的人。 重复几次，直到所有人同意这个数组是排序好的。

 

 

智能设计排序

 

无论你的数组状态是什么样的，它都算是排好序的。 解释：原始输入按照某种顺序的概率是 1/(n!)。概率是如此小，（当前的顺序）归结于运气成分显然是荒谬的，所以它是按照“智能设计”排序过的。所以完全可以说数组已经排好序了，只是不是我们传统意义上的“升序”。如果按照我们传统观点对它进行操作，只会让它乱序。（“智能设计”涉及宗教和哲学，不过多解释）

 

 

互联网排序

 

这是一种冒泡排序，但每次比较都依靠互联网的搜索。比如 “0.211 和 0.75 哪个大？”

 

 

委员会排序

 

排序一个包含 N 个自然数的数组，首先用纸打印出 N 份整个数组。 然后在办公室周围选择几个恰好路过的倒霉委员。每个委员对应数组中的一个数字。 给每个委员一份打印的数组，并让他们通过开会或其他手段，来决定自己代表的数字应该在有序数组中的位置。 当这些委员有结论并答复你时，数组自然排好序了。

---

---